[ NLP ] 텍스트 유사도 ( 유클리디언 유사도, 맨하탄 유사도 )

앞의 게시글의 예문만 가져와서 확인해 보겠다.

• 휴일인 오늘도 서쪽을 중심으로 폭염이 이어졌는데요, 내일은 반가운 비 소식이 있습니다.
• 폭염을 피해서 휴일에 놀러왔다가 갑작스런 비로 인해 망연자실하고 있습니다.

3. 유클리디언 유사도

: 가장 기본적인 거리를 측정하는 유사도 공식

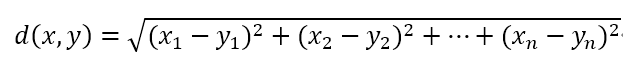
유클리디언 유사도 공식

 

여기서 구하는 거리는 유클리디언 거리 혹은 L2 거리 라고 불리며, n차원 공간에서 두 점 사이의 최단 거리를 구하는 접근법.

from sklearn.metrics.pairwise import euclidean_distances

euclidean_distances(tfidf_matrix[0:1], tfidf_matrix[1:2])

array([[1.28099753]])

앞 서 확인했던 유사도 방식들은 모두 0과 1 사이의 값을 가지는데 이건 1보다 크게 나왔다. 이것은 단순히 두 점 사이의 거리를 뜻하기 때문에 값에 제한이 없기 때문이다.

 

이런 제한이 없다면 사용하기 어렵기에 제한해야한다. 앞서 각 문장을 벡터화 했는데 일반화한 후 다시 유클리디언 유사도로 측정하면

0과 1사이의 값을 갖게 된다. 여기서는 L1 정규화 방법을 사용할 것이다.

(L1 정규화 방법 : 각 벡터 안의 요소 값을 모두 더한 것의 크기가 1이 되도록 벡터들의 크기를 조절하는 방법)

 

import numpy as np

def l1_normalize(v):
    norm=np.sum(v)
    return v/norm

tfidf_norm_l1=l1_normalize(tfidf_matrix)
euclidean_distances(tfidf_norm_l1[0:1],tfidf_norm_l1[1:2])

array([[0.20491229]])

4. 멘하탄 유사도

: 맨하탄 거리를 통해 유사도를 측정하는 방법

 

맨하탄 거리란 사각형 격자로 이뤄진 지도에서 출발점에서 도착점까지를 가로지르지 않고 잘 수 있는 최단거리를 구하는 공식

유클리디언 거리는 L2라고 부르지만 맨하탄 거리는 L1 거리라고 부른다.

맨하탄 거리 공식

사각형 격자 거리 구하기

 

위 그림에서 유클리디언 거리는 검은선을 의미한다. 하지만 장애물이 없다고 가정한 것이기에 현실성은 없다.

가장 적합한 맨하탄 거리는 빨간색을 의미하며, 도로를 감안해서 가장 짧은 거리의 길이라고 생각하면 된다.

 

맨하탄 유사도 역시 값이 계속해서 커질 수 있으므로 L1 정규화 방법으로 정규화 한 뒤 유사도를 축정한다.

 

from sklearn.metrics.pairwise import manhattan_distances

manhattan_distances(tfidf_norm_l1[0:1],tfidf_norm_l1[1:2])

array([[0.77865927]])

 

맨하탄 유사도로 측정했을 때 유사도가 가장 높게 나왔는데 측정 방법에 따라 유사도가 다르므로 의도하고자 하는 방향에 맞는 유사도 측정 방법을 고르는 것이 중요하다.